Don’t FOIL, learn the distributive property instead

Thinking back to my early math education, it felt like there was a single day dedicated to the three basic properties of numbers (associative, commutative, and distributive), but more than a week for “FOIL”. In retrospect, this feels backwards—like it foiled the learning process.

FOIL is a trick for multiplying two sums: (a + b)(c + d). It’s an acronym that stands for First, Outer, Inner, Last. All you have to do is follow the rules and not think too much about it:

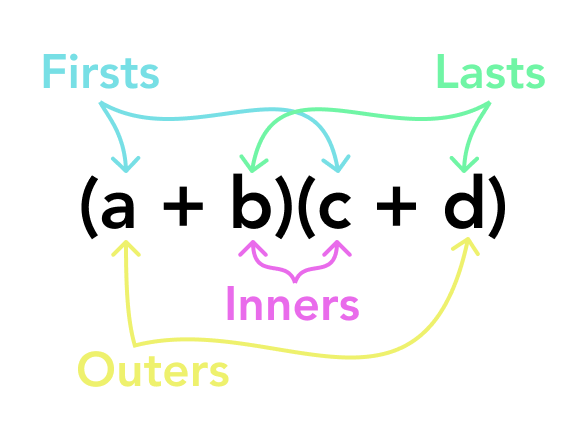
which gives us:

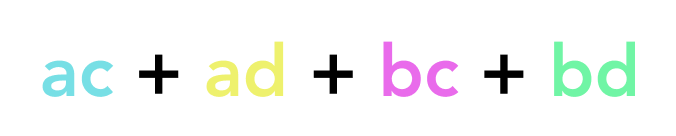
Unfortunately, there’s no understanding with FOIL. It’s unclear why it works and if you encounter something a little different—like (a + b + c)(d + e)—then you don’t have the tools to handle this curveball.

However, going back to our three basic properties of numbers and looking specifically at the distributive property, we can come up with a generalized approach that doesn’t require remembering any tricks.

With the distributive property “multiplication distributes over addition”, but more simply it looks like this:

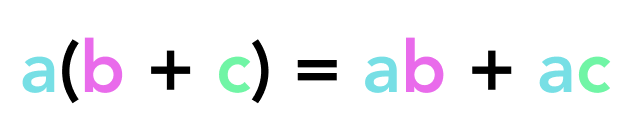
If we step back to our multiplication of sums (a + b)(c + d) and we imagine (a + b) as one variable, then we suddenly see something that looks exactly like the distributive property! Essentially, we just apply the distributive property twice:

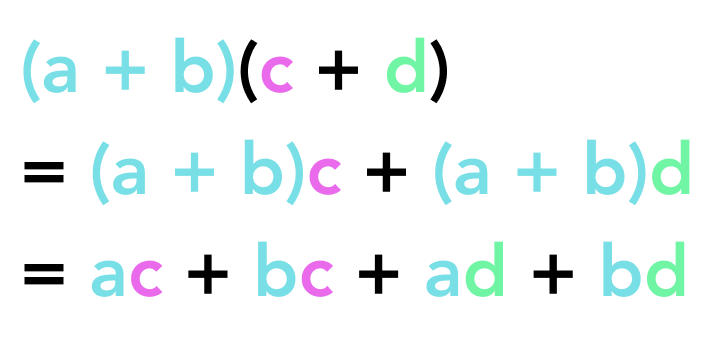
By building an understanding for the distributive property, we don’t need to learn FOIL, and even better, we understand why FOIL works. When you’re able to apply an abstract concept in math, it suddenly shifts from being a tricky set of rules to follow, to becoming an empowering tool to think through and solve problems that you haven’t even seen before!

More so, you can see flavors of the distributive property in other tricky concepts taught in early math. For example, in long division, you end up working you way down the digits of the number being divided in a way that ends up looking like the distributive property in reverse. With 435 / 5, you extract 80 and 7, to get 87, which means we can represent 435 as: 5 * 87 = 5 * (80 + 7) = 5*80 + 5*7.

I think more of a focus on abstract concepts would help a lot of kids crack higher levels of math and feel more empowered in the classroom. FOIL should be a brief mention, while the basic properties of numbers should be many weeks of instruction. Obviously, I’m not a teacher, have no education in teaching, and have not been put in the position to try and teach a classroom of elementary school students or middle schoolers how to multiply sums of numbers. Also in my first go at thinking through this, I thought the distributive property was the first really abstract concept students encounter in math, but I quickly realized that order of operations (Please Excuse My Dear Aunt Sally) is a surprisingly abstract concept that is really fundamental to all of this (and I can excuse the dear acronym in this situation). On top of that, instruction on this material must be way more nuanced in practice and ultimately require way more individualization for different types of learners, and I’d love to hear ideas from actual math teachers on when FOIL might be helpful and when it can be dumped.